Introduction

$DiscretePOMP.jl$ is a package for:

• Bayesian parameter inference, and
• Simulation of,
• Discrete-state-space Partially Observed Markov Processes, in Julia.
• It also includes automated tools for things like convergence diagnosis, model assessment and analysis.

What are DPOMP models?

Discrete-state-space (DSS) models are used throughout ecology and other scientific domains to represent systems comprised of interacting components (e.g. people or molecules.)

A well-known example is the Kermack-McKendrick susceptible-infectious-susceptible (SIR) model:

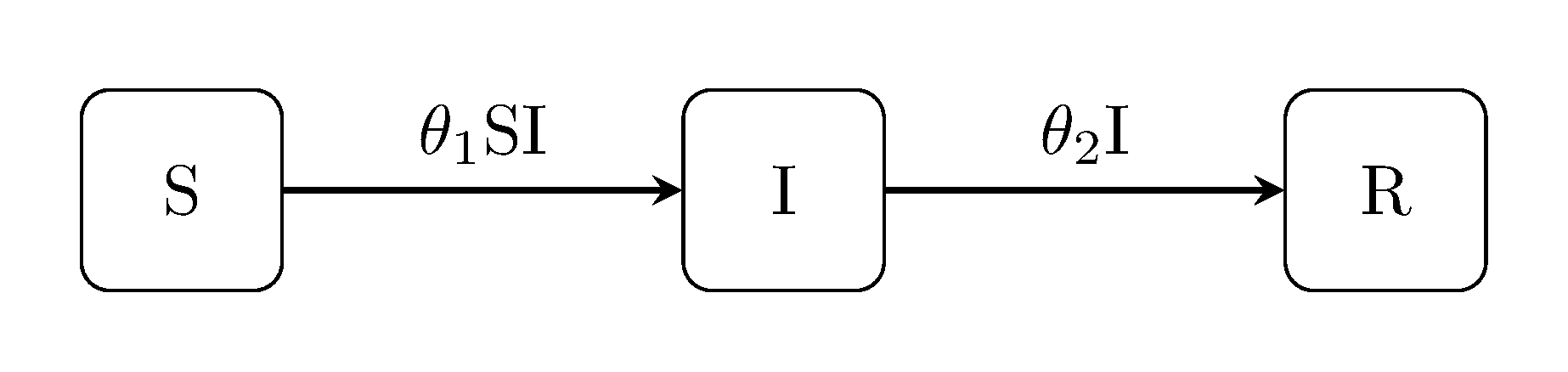
See the Simple example for a brief primer on DSS.

In applied situations (e.g. like a scientific study) such systems are often difficult to directly observe, and so they are referred to in context as being Partially Observed.

The dynamics (how the system changes over time) of the SIR, and other DSS models, can be represented in continuous time by [a set of coupled] Markov Processes. More specifically, we can define a probability density (a 'likelihood function' in Bayesian parlance) that governs the time-evolution of the system under study.

Combining these concepts, we have a general class of statistical model: Discrete-state-space Partially Observed Markov Processes, or Discrete POMP.

Furthermore, given some applicable [partially complete] scientific data, they yield a paradigm for (in this case, Bayesian) statistical inference based on that model class. That is, we can infer [the likely value of] unknown quantities, such as the unknown time of a known event (like the introduction of a pathogen,) or a model parameter that characterises the infectiousness of that pathogen.

To summarise, DPOMP models and associated methods allow us to learn about a given system of interest (e.g. an ecosystem, pandemic, chemical reaction, and so on,) even in when the available data is limited ['partial'].

Scientific applications

Discrete POMP, and discrete-state-space models in general, have a wide range of applications including:

• Epidemiological modelling (e.g. SEIR models)
• Ecology (e.g. predator-prey dynamics)
• Many other potential use cases, e.g. physics; chemical reactions; social media.

Package features

The algorithms implemented by the package for simulation and inference include:

• The Gillespie direct method algorithm
• Data-augmented Markov chain Monte Carlo (MCMC)
• The model-based-proposal (MBP) algorithm^[1]
• Particle filters (i.e. Sequential Monte Carlo)
• SMC^2^[2], or iterative-batch-importance sampling (IBIS)

A number of well-known models are provided as predefined examples:

• SIR, SEIR, and other epidemiological model
• The Lotka-Voltera predator-prey model
• Ross-MacDonald two-species malaria model

The package code was initially developed during the course of a postgraduate research project in infectious disease modelling at Biostatistics Scotland, and there is a heavy emphasis on epidemiology and epidemiological modelling throughout.

In practice though, this affects only the applied examples and naming conventions of the predefined models available with the package. Otherwise, the models and methods are applicable to many situations entirely outwith the field of ecology (such as chemical reactions.)

Installation

As a prerequisite, the package naturally requires a working installation of the Julia programming language. The package is not yet registered but can nonetheless must be added via the package manager Pkg in the usual way.

From the $Julia$ REPL, run:

using Pkg
Pkg.add(url="https://github.com/ScottishCovidResponse/DataRegistryUtils.jl")

See the package code repository to inspect the source code.

Documentation

• Models
• Predefined models
• Customising predefined models
• Custom models from scratch
• Model directory
• Simple example
• Introduction
• Defining models
• Simulation
• Inference
• Model comparison
• Package manual
• Types
• Functions
• Index