Models

This section provides instructions for generating model instances in DiscretePOMP.jl.

Predefined models

The package includes a set of predefined models, which can be instantiated easily:

using DiscretePOMP      # simulation / inference for epidemiological models
import Distributions    # priors

model = generate_model("SIS", [100,1])

Customising predefined models

DPOMPModels are mutable $structs$, which means that their properties can be altered after they have been instantiated. For example, we could specify a prior:

model.prior = Distributions.Product(Distributions.Uniform.(zeros(2), [0.01, 0.5]))

Custom models from scratch

Models can also be specified manually. For example, the model we just created could also be instantiated like so:

# rate function
function sis_rf!(output, parameters::Array{Float64, 1}, population::Array{Int64, 1})
    output[1] = parameters[1] * population[1] * population[2]
    output[2] = parameters[2] * population[2]
end
# define obs function
function obs_fn(y::Observation, population::Array{Int64, 1}, theta::Array{Float64,1})
    y.val .= population
end
# prior
prior = Distributions.Product(Distributions.Uniform.(zeros(2), [0.01, 0.05]))
# obs model
function si_gaussian(y::Observation, population::Array{Int64, 1}, theta::Array{Float64,1})
    obs_err = 2
    tmp1 = log(1 / (sqrt(2 * pi) * obs_err))
    tmp2 = 2 * obs_err * obs_err
    obs_diff = y.val[2] - population[2]
    return tmp1 - ((obs_diff * obs_diff) / tmp2)
end
tm = [-1 1; 1 -1] # transition matrix
# define model
model = DPOMPModel("SIS", sis_rf!, [100, 1], tm, obs_fn, si_gaussian, prior, 0)

Model directory

Here we provide a brief overview of predefined models available in the package.

Epidemiological models

SIR model

The canonical Kermack-McKendrick susceptible-infectious-recovered model is perhaps the best known example of state-space models used within the field of epidemiology.

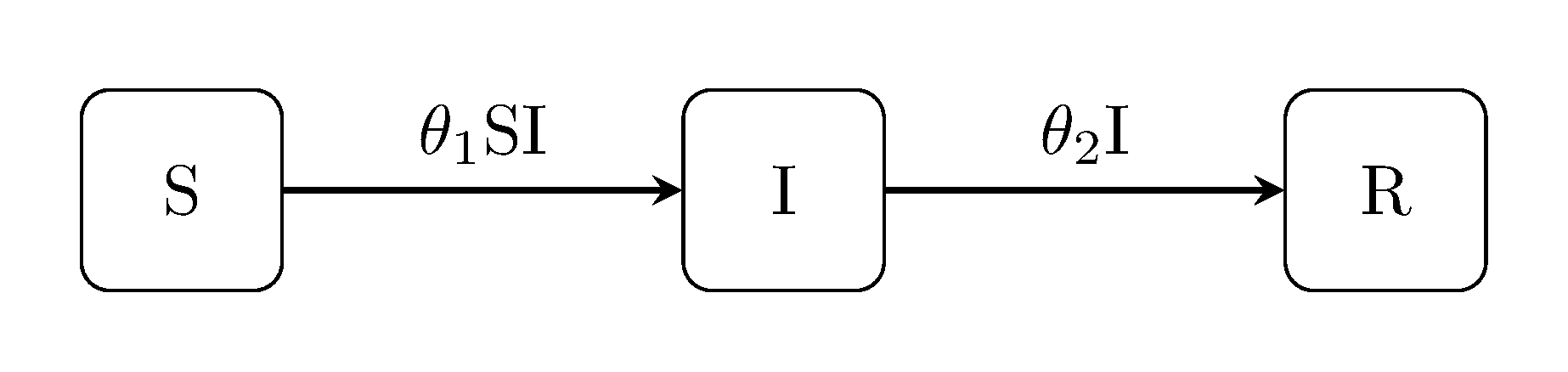
generate_model("SIR", [100, 1, 0])

SI model

The susceptible-infectious model is the simplest conceptual example of this class of model; two states and only one type of event.

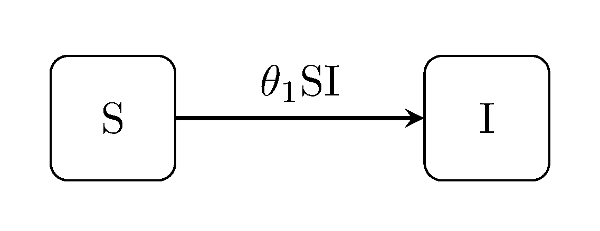
generate_model("SI", [100, 1])

SIS model

Another common derivative of the SIR model.

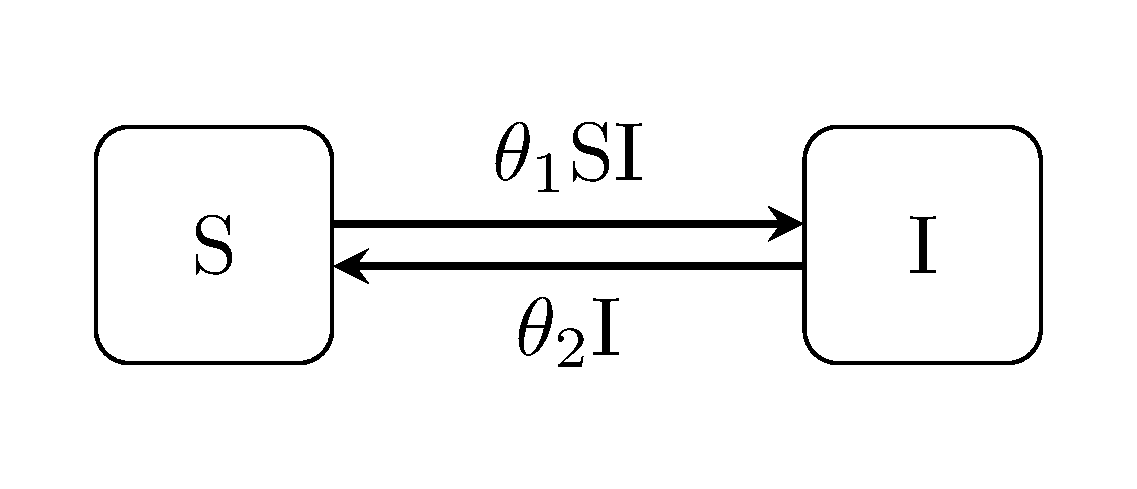
generate_model("SIS", [100, 1])

SEI model

The SEI model includes an 'exposed' state, i.e. for modelling communicable diseases with latent non-infectious periods.

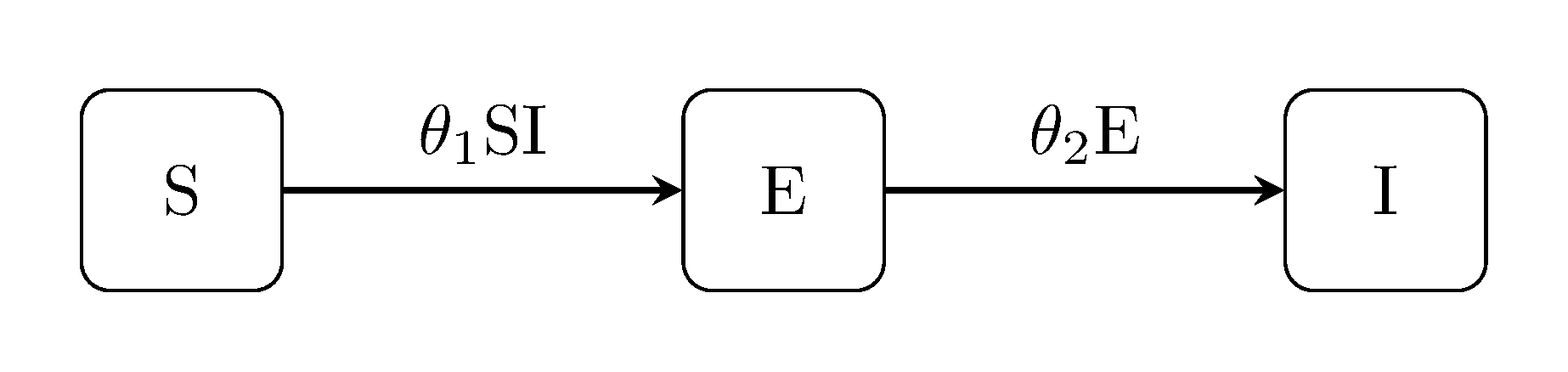
generate_model("SEI", [100, 0, 1])

SEIR model

Somewhat obviously, the SEIR model concept combines the SEI with the SIR.

generate_model("SEIR", [100, 0, 1, 0])

Others

The Lotka-Volterra predator-prey model

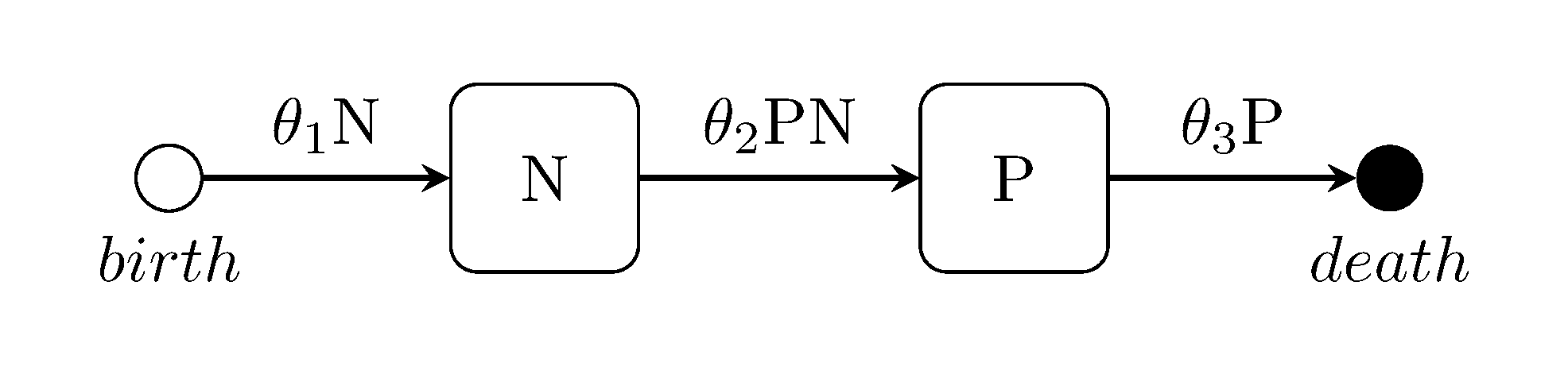
generate_model("LOTKA", [70, 70])

Ross-MacDonald two-species Malaria model

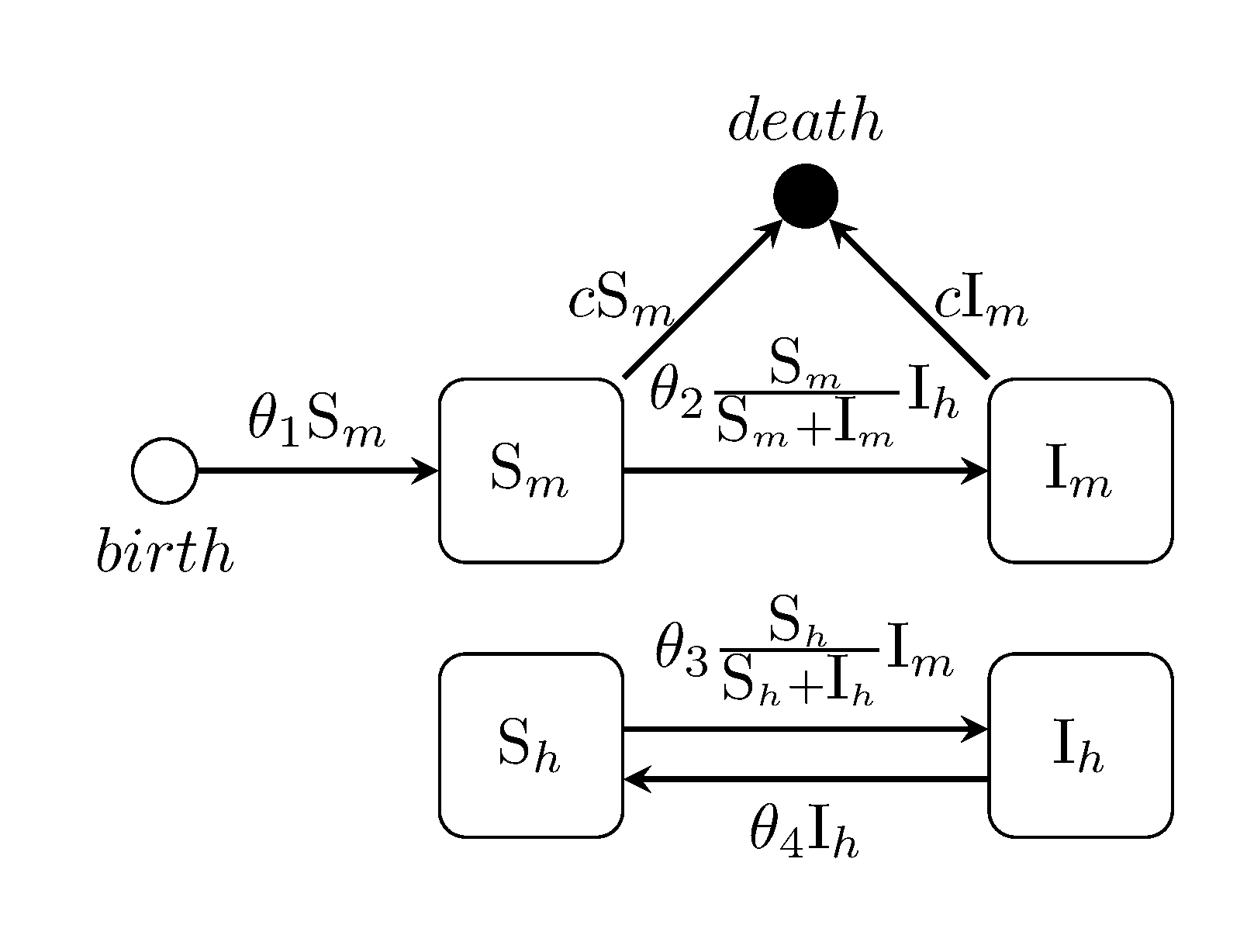
generate_model("ROSSMAC", [100, 0, 400, 50])